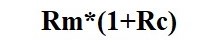The “Cowley” model is an economic model whose purpose is to calculate the level of risk concerning market prices by the analysis of internal variables in the business and the degree of influence of macroeconomic and sectorial (external) variables on the business as well. The purpose of the model is to determine the success or risk rates of businesses or companies, either private or public.
The model is based on the analysis of periodic balance sheets and comparing its internal and external variables in given periods. Also, evaluation functions for determining the risk values are changeable factors between industries and businesses, according to formulas based on economic and mathematical models.
Below is the generic formula of the model:
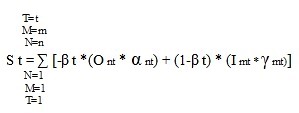
St – aggregate test result at a given point in time. In the case of time series, we will get T=1 to T=T, and the relative weights will be a function of the dependence between the objective variables and the intra-organizational variables through expressions of different types of functions that are not necessarily linear. An autonomous factor A can be added to the equation in case of time series and random variables.
O- is a given objective variable. Its values are between 0 and 10, where it receives the negative sign through the negative values of the external variables (which are measured by their level of influence in absolute values).
α – is the relative weight of objective factor N where ∑ α from 1 to n, sums up to α = 1
β – the relative weight between the objective factors and the internal factors. Condition – β=> 0 and less than 1
I – is an internal variable within organizations given the condition I <=10>=zero
γ – is the relative weight of the internal-organizational factor when ∑ γ from 1 to m, sums up to – γ = 1
N – the number of objective (external) variables
M – the number of intra-organizational variables
T – the date of the test. We build time series and look for the relations between them and thus find their weights or functions.
The formula for converting the calculation result into a success rate is as follows:
P = (Ab + St)/20 where P is the success rate and St is the result of the calculation according to the listed formula. Ab is the autonomous value which determines the basic survival rate of firms in the sample. When the value of Ab is 10, the basic survival rate is 50% (A).
In the same way, the expectancy of the risk coefficient (1-P) can be calculated and changed according to the basic rate of the autonomous risk (1-A), when Rc is the adjustment coefficient of the interest rate for the markets’ rate.
The final formula of the capitalization rate is as follows: